Measuring Gravity From a Moving Aircraft

From: Joël Dubé, Engineer/Geophysicist at Sander Geophysics, OIB P-3 Gravity Team

One of the instruments used in Operation IceBridge (OIB) is an airborne gravimeter operated through a collaboration between Lamont Doherty Earth Observatory of Columbia University and Sander Geophysics. Some people from other instrument teams call it a gravity meter, gravity, gravitometer, gravy meter, gravel meter, gravitron, or blue couch-like instrument. As operators of the gravimeter, we are referred to as graviteers, gravi-geeks or gravi-gods. This tells a lot about how mysterious and unknown this technology appears.

Let me summarize the basics of airborne gravity data acquisition for you.

But first, why is gravity data being acquired as part of OIB?

The earth’s gravity field is varying in space according to variations in topography and density distribution under the earth’s surface. Essentially, the greatest density contrast is between air (0.001 g/cc), water and ice (1.00 and 0.92 g/cc, respectively) and rocks (2.67 g/cc in average). Therefore, gravity data can be used for modelling the interface between these three elements. The ATM system (laser scanner) can locate the interface between air and whatever is underneath it with great accuracy. The MCoRDS system (ice penetrating radar) is successful at locating the interface underneath the ice. However, no radar system can “see” through water from the air. Hence, gravity data can help determine bathymetry beneath floating ice, either off shore or on shore (sub-glacial lakes). This in turn enables the creation of water circulation models and helps to predict melting of the ice from underneath. Also, airborne gravity data can contribute to increasing the accuracy and resolution of the Earth Gravitational Model (EGM), which is determined only with low resolution in remote locations such as the poles, being built mainly from data acquired with satellites.

Most people don’t know that it is possible to acquire accurate gravity data from a moving platform such as an aircraft. Due to the vibrations and accelerations experienced by the aircraft, it is definitively a challenge! There are four key elements that make this possible.

1- You must have very accurate acceleration sensors, called accelerometers.

2- You must keep these accelerometers as stable as possible, and oriented in a fixed direction. This is a job for gyroscopes coupled with a system of motors that keeps the accelerometers fixed in an inertial reference frame, independently of the attitude of the aircraft. This is why the system we use is called AIRGrav, which stands for Airborne Inertially Referenced Gravimeter. Damping is also necessary to reduce transmission of aircraft vibrations to the sensors. The internal temperature of the gravimeter also has to be kept very stable.

This is all good. However, the accelerations we are measuring this way are not only due to the earth’s gravity pull, but also (and mostly) due to the aircraft motion. And to correct for that:

3- You need very accurate GPS data, so that you can model the aircraft motion with great precision.

Despite these best efforts, noise remains, mostly from GPS inaccuracies and aircraft vibrations that can’t be detected by GPS, so:

4- You have to apply a low pass filter to the data, since the noise amplitude is greatest at high frequency.

The AIRGrav system on-board the P-3 aircraft. Gravimeter (right), rack equipped with computers controlling the gravimeter and GPS receivers (center) and operator (left). Credit: Joël Dubé

Furthermore, a number of corrections have to be applied to the data before they can serve the scientific community. The corrections aim at removing vertical accelerations that have nothing to do with the density distribution at the earth’s sub-surface.

The Latitude correction removes the gravity component that is only dependent on latitude. That is the gravity value that would be observed if the earth was treated as a perfect, homogeneous, rotating ellipsoid. This value is also called the normal gravity. Since the earth is flatter at the poles, being at high latitude means you are closer to the earth’s mass center, hence the stronger gravity. Also, because of the earth’s rotation and the shorter distance to the spinning axis, a point close to the pole moves slower and this will add to gravity as well (less centrifugal force acting against earth’s pull).

Anything traveling in the same direction as the earth’s rotation (eastward), will experience a stronger centrifugal force thus a weaker gravity, and the other way around in the other direction. Traveling over a curved surface also reduces gravity no matter which direction is flown, similar to feeling lighter on a roller coaster as you come over the top of a hill. This is known as the Eötvös effect and is taken care of by the Eötvös correction. This correction is particularly important for measurements taken from an aircraft moving at 250-300 knots.

The Free Air correction simply accounts for the elevation at which a measurement is taken. The further you are from the earth’s center, the weaker the gravity.

To give you an idea of how small the gravity signal that we are interested in is with respect to other vertical accelerations that have to be removed, let’s look at the following profiles made from a real data set. All numbers are in mGals (1 m/s2 = 100,000 mGals), except for the terrain and flying height which are in meters.

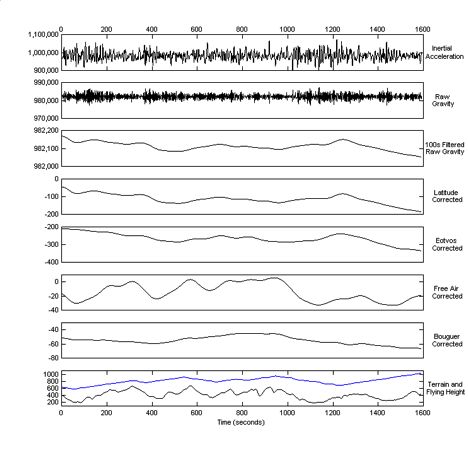
A visual summary of gravity corrections. Credit: Stefan Elieff

“Raw Gravity” in this diagram means that GPS accelerations (aircraft motions) have been removed from inertial accelerations. Notice the relative scales of the profiles, starting at 200,000 mGals, down to 20,000 mGals when aircraft motions are accounted for, down to 200 mGals after removing most of the high frequency noise, and ending at 50 mGals for Free Air corrected gravity. Free Air gravity is influenced by the air/water/ice/rock interfaces described earlier, and since OIB uses the gravity data to find the rock interface (the unknown), Free Air gravity is the final product. As a side note, for other types of gravity surveys, we usually want to correct for the terrain effect (the air/water/rock interfaces are known in these cases), so that we are left with the gravity influenced only by the variations of density within the rocks. This is called Bouguer gravity and is also shown in the figure.

Notice the inverse correspondence between flying height (last profile, in blue) and the profiles before the free air correction (going higher, further from the earth, decreases gravity), and the correspondence between terrain (last profile, in black) and the free air corrected data.

Now, let’s look at some data acquired during the current 2011 mission in western Greenland.

Ice elevation (left), rock elevation (middle) and Free Air gravity data (right). Greenland 2011 flight lines shown in black. Gravity data is preliminary and is not yet available for scientific analysis.

The left panel shows the elevation of the rocks, or of the ice where ice is present. It is as if the water has been drained from the ocean. The middle panel shows only the bedrock elevation, both ice and water being removed. The data is from ETOPO1, a global relief model covering the entire earth. The right panel shows the Free Air gravity acquired in the last few weeks. Most channels, called fjords, are well mapped by the gravity data. It is interesting to see that the gravity data infers the presence of a sub-glacial channel (shown by the red arrow) where no channel is mapped (yet?) on the bedrock map. The most likely reason for this is that this particular region has not been covered by previous ice radar surveys (there are huge portions of the Greenland ice sheet that remain unexplored). Note that the MCoRDS ice radar data acquired as part of the current campaign will improve the resolution in this area and will enable for a better comparison of both data sets in the future.